박스플롯과 산점도 결합차트 그리기

개요

이번 글에서는 박스플롯(Boxplot)과 산점도(Scatter plot)를 결합한 차트를 소개합니다. 박스플롯은 데이터의 중앙값, 사분위수(IQR), 이상치 등을 요약적으로 시각화하여 데이터의 전반적인 분포와 중심 경향을 파악할 수 있는 차트입니다. 이를 통해 여러 그룹 간 데이터 분포를 직관적으로 비교하거나 이상치를 탐지하는 데 효과적입니다. 반면 산점도는 개별 데이터 포인트의 위치와 밀집도를 세부적으로 보여주는 차트로, 데이터의 세부적인 분포를 직관적으로 이해할 수 있도록 돕습니다.

박스플롯은 데이터의 요약 정보를 제공하는 데 유용하지만 개별 데이터 포인트의 위치를 직접 보여주지는 않습니다. 이때 산점도를 결합하면 데이터의 요약 정보와 세부 분포를 동시에 확인할 수 있어 데이터 분석에 있어 더 풍부한 통찰을 제공합니다. 이번 글에서는 2023년 기준 시도별 청년인구 비율을 분석하여 이러한 차트를 그려보겠습니다.

데이터 준비하기

먼저, 필요한 패키지를 로드하고 차트에 사용할 글꼴을 설정합니다.

# 패키지 로드
library(tidyverse)
library(readxl)
library(ggplot2)
library(showtext)
library(scales)

# 글꼴 설정
font_add("kopub", "C:/Users/.../AppData/Local/Microsoft/Windows/Fonts/KoPub Dotum Medium.ttf")
showtext_auto()
showtext_opts(dpi=300)

theme.size = 12
text.size = theme.size / .pt

2023년 기준 시도별 청년인구 비율을 구하기 위해 통계청의 행정구역(읍면동)별/5세별 주민등록인구(2011년~) 자료를 활용합니다.

# 데이터 불러오기
pop <- read_xlsx("데이터/시도 인구 특성/5세별주민등록인구_시도_2023.xlsx")

청년인구는 만 20~34세로 정의하며, 이를 기준으로 청년인구 수와 전체인구 수를 계산한 후 비율을 구합니다.

# 청년 정의
age <- unique(pop$`5세별`)
youth <- age[5:6]

# 5세별 주민등록인구 데이터 가공하기
pop_sum <- pop %>% 
  rename(시도 = `행정구역(동읍면)별`) %>% 
  mutate(구분 = case_when(`5세별` %in% youth ~ "청년인구 수",
                        T ~ "그 외 인구 수")) %>% 
  group_by(시도, 구분) %>% 
  summarise(`인구 수` = sum(`2023`, na.rm = T)) %>% 
  pivot_wider(id_cols = 시도, names_from = 구분, values_from = `인구 수`) %>% 
  mutate(`인구 수` = `청년인구 수` + `그 외 인구 수`,
         `청년인구 비율` = `청년인구 수` / `인구 수`) %>% 
  select(-`그 외 인구 수`) %>% 
  filter(시도 != "전국")

# 데이터 확인하기
head(pop_sum)

## # A tibble: 6 × 4
## # Groups:   시도 [6]
##   시도           `청년인구 수` `인구 수` `청년인구 비율`
##   <chr>                  <dbl>     <dbl>           <dbl>
## 1 강원특별자치도        163610   1527807          0.107 
## 2 경기도               1682138  13630821          0.123 
## 3 경상남도              322711   3251158          0.0993
## 4 경상북도              248255   2554324          0.0972
## 5 광주광역시            190905   1419237          0.135 
## 6 대구광역시            282470   2374960          0.119

박스플롯 구성요소 이해하기

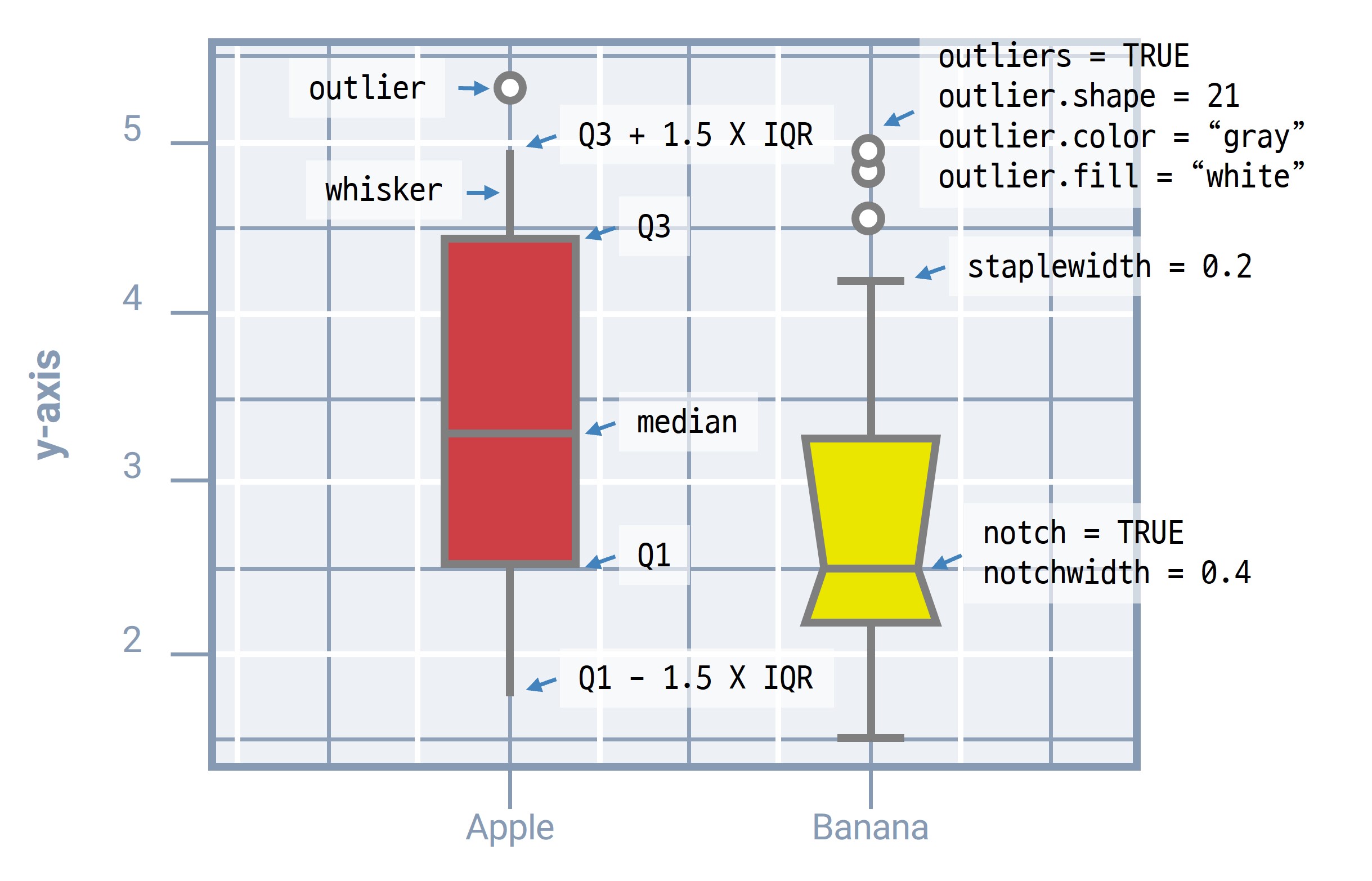
박스플롯 구성요소로 박스(box), 수염(whisker), 중앙값(median), 이상치(outliers), 끝선(staple), 중앙값 노치(notch) 등이 있습니다.

박스: 중앙값을 기준으로 1사분위수(Q1)와 3사분위수(Q3) 사이의 범위를 보여줍니다. 이 영역은 데이터의 중간 50%를 나타내며, 사분위 범위(IQR)라고도 합니다.
수염: 데이터의 주요 범위를 나타냅니다. 수염의 끝은 Q1과 Q3에서 IQR의 1.5배 내외에 위치하는 데이터를 가리킵니다. 기본값은 1.5배지만, coef 파라미터로 조정할 수 있습니다.
끝선: 수염의 끝에 짧은 선으로 표시되며, 수염의 끝을 명확히 보여줍니다.
이상치: 수염 바깥에 위치한 데이터 포인트를 점으로 표시합니다.
중앙값: 박스 안의 굵은 선으로 표시되며, 데이터의 중앙값을 나타냅니다.
중앙값 노치: 중앙값 주위의 좁아진 영역으로, 그룹 간 중앙값을 시각적으로 비교할 때 유용합니다.

박스플롯 구성요소

박스플롯 그리기

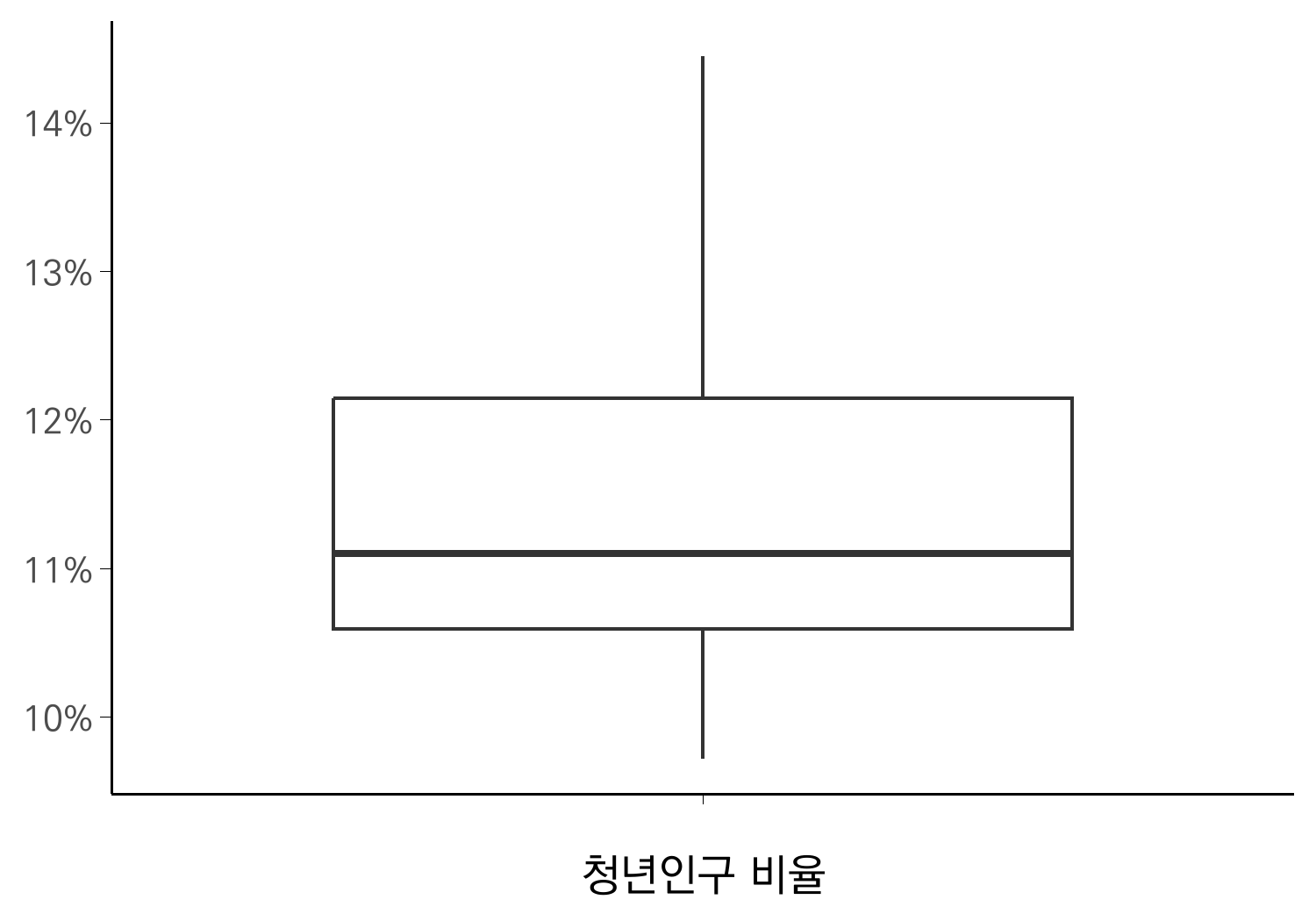
가장 기본적인 박스플롯을 먼저 그려봅니다. 박스플롯은 데이터의 중앙값과 사분위수 범위를 요약적으로 보여줍니다.

ggplot(pop_sum,
       aes(x = "", y = `청년인구 비율`)) +
  geom_boxplot() +
  scale_x_discrete(name = "청년인구 비율") +
  scale_y_continuous(labels = percent_format(accuracy=1)) +
  theme_minimal(base_size = theme.size, base_family = "kopub") +
  theme(
    axis.title.y = element_blank(),
    axis.line = element_line(linewidth = 0.4),
    axis.ticks = element_line(linewidth = 0.1),
    panel.grid = element_blank(),
  )

기본 박스플롯

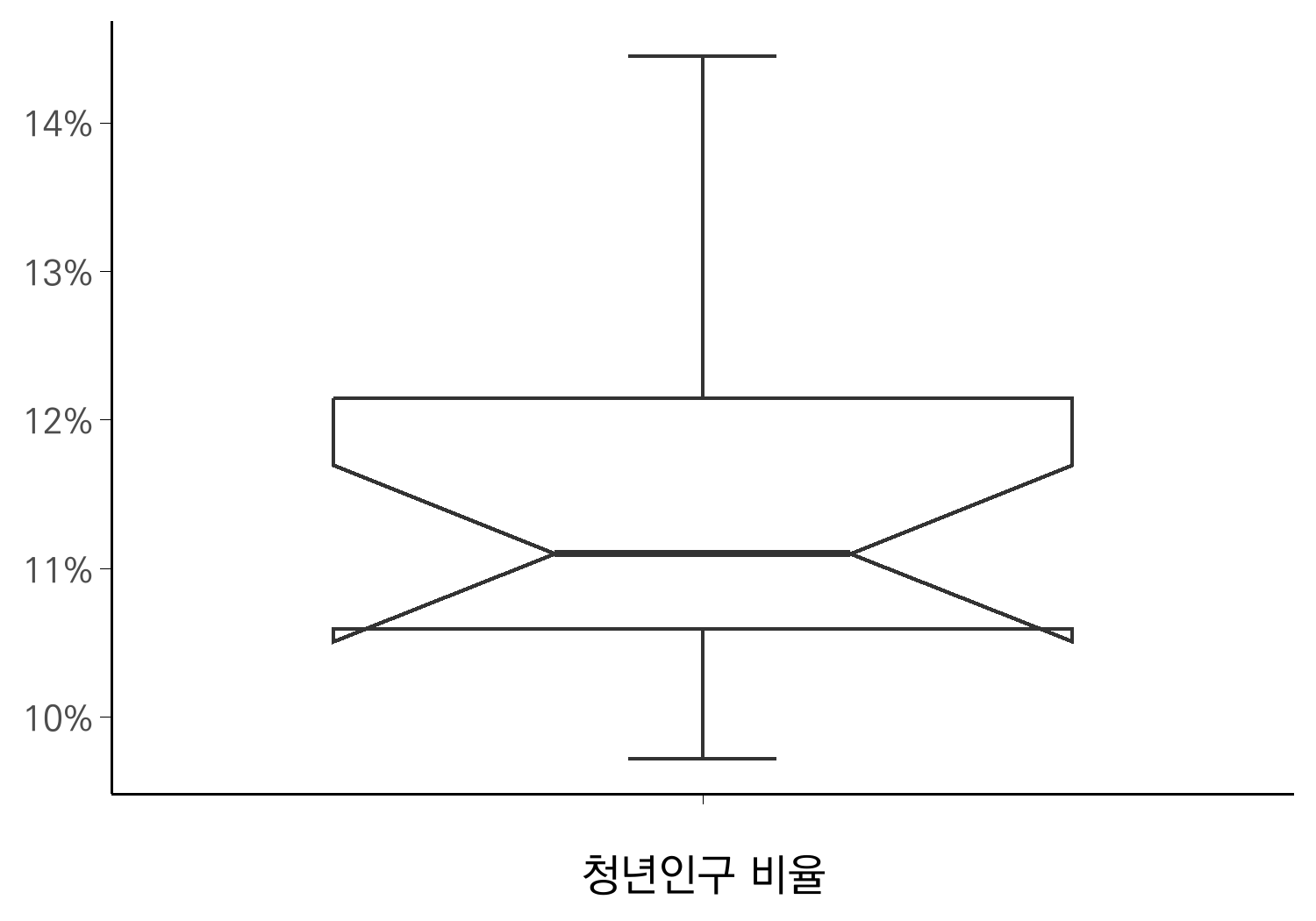
기본 박스플롯에 끝선을 추가하고, 노치를 설정하면 다음과 같이 나타납니다.

ggplot(pop_sum,
       aes(x = "", y = `청년인구 비율`)) +
  geom_boxplot(
    staplewidth = 0.2,
    notch = TRUE,
    notchwidth = 0.4
  ) +
  scale_x_discrete(name = "청년인구 비율") +
  scale_y_continuous(labels = percent_format(accuracy=1)) +
  theme_minimal(base_size = theme.size, base_family = "kopub") +
  theme(
    axis.title.y = element_blank(),
    axis.line = element_line(linewidth = 0.4),
    axis.ticks = element_line(linewidth = 0.1),
    panel.grid = element_blank(),
  )

수정한 박스플롯

산점도 추가하기

박스플롯에 개별 데이터 포인트를 추가하려면 geom_jitter를 사용합니다. 이 함수를 통해 포인트를 박스플롯 위에 적절히 분산 배치할 수 있습니다.

width와 height를 기본값으로 두면, 포인트가 80% 범위 내에서 무작위로 분산됩니다. 이 둘을 0.5로 설정하면 포인트가 넓게 퍼져서 범주 간 구분이 어려워질 수 있으므로, 좀더 좁은 범위 내에서 무작위 분산하도록 지정해야 합니다. 본 예제에서는 비교 대상이 되는 다른 그룹이 있는 것은 아니지만, 좀 더 좁은 범위에서 데이터가 표시되도록 width = 0.2로 지정하겠습니다. 또한, 포인트 사이즈를 키우고 색상과 투명도를 조정하겠습니다.

ggplot(pop_sum,
       aes(x = "", y = `청년인구 비율`)) +
  geom_boxplot(
    staplewidth = 0.2
  ) +
  geom_jitter(
    width = 0.2,
    size = 3,
    color = "gray20",
    alpha = 0.4
  ) +
  scale_x_discrete(name = "청년인구 비율") +
  scale_y_continuous(labels = percent_format(accuracy=1)) +
  theme_minimal(base_size = theme.size, base_family = "kopub") +
  theme(
    axis.title.y = element_blank(),
    axis.line = element_line(linewidth = 0.4),
    axis.ticks = element_line(linewidth = 0.1),
    panel.grid = element_blank(),
  )

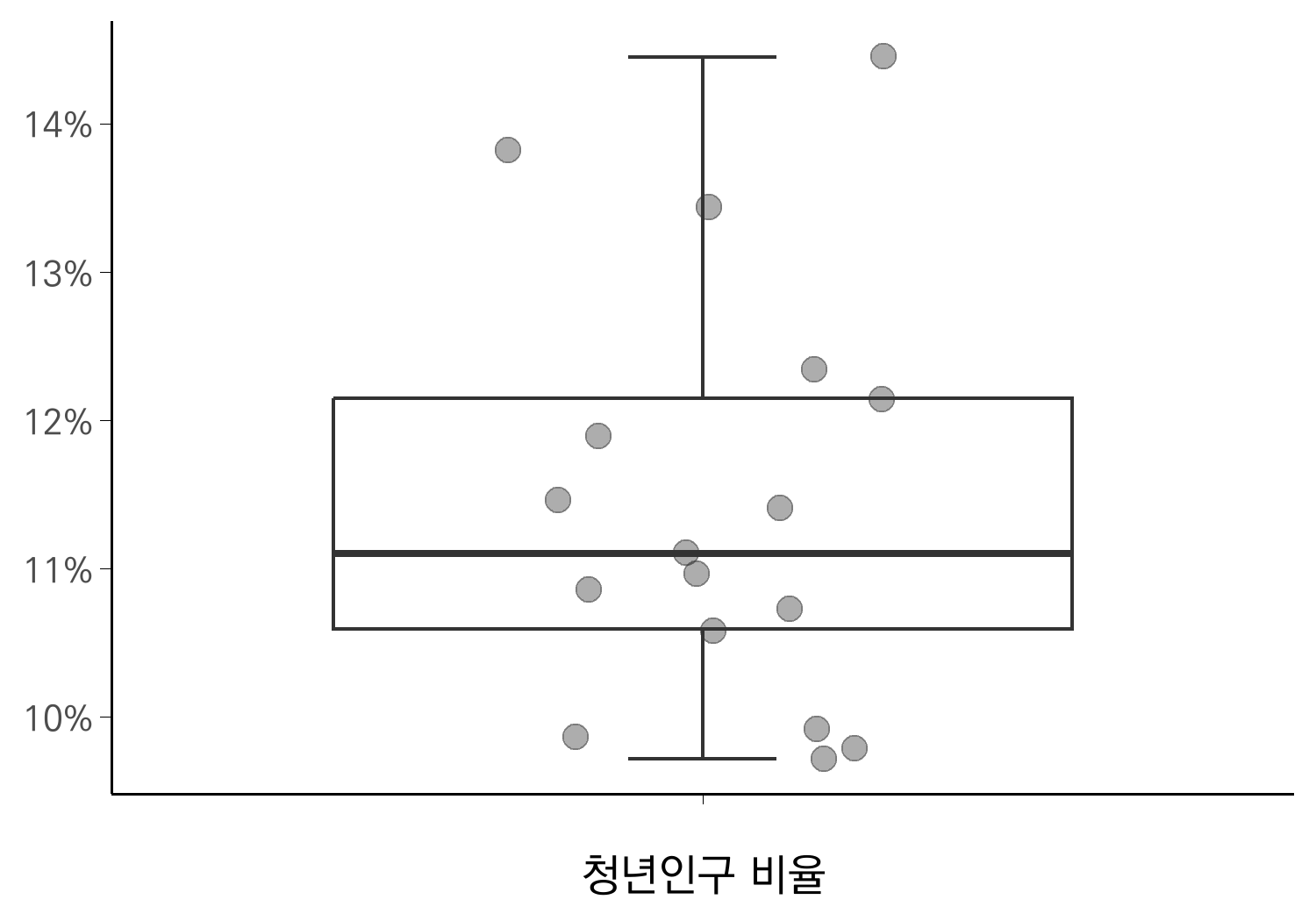
산점도를 추가한 박스플롯

이처럼 박스플롯과 산점도를 결합하면 데이터의 전체적인 분포와 세부적인 위치를 동시에 파악할 수 있습니다. 박스플롯은 데이터를 요약적으로 보여주고, 산점도는 개별 데이터 포인트를 시각화하므로 서로 보완적인 역할을 합니다. 이 두 차트를 조합하면 그룹 간 분포를 더 효과적으로 비교하고, 데이터의 세부적인 특징을 살펴볼 수 있으니 한 번 활용해 보세요!